神经网络和BP算法推导

感知机

感知机（perceptron）于1957年由Rosenblatt提出，是一种二分类线性模型。感知机以样本特征向量作为输入，输出为预测类别，取正、负两类。感知机最终学习到的是将输入空间（特征空间）划分为正、负两类的分离超平面，属于判别模型。为此，使用误分类作为损失函数，利用梯度下降优化该函数，可求得感知机模型。感知机是神经网络与支持向量机的基础。

单层感知机

第 ${i}$ 个样本的预测值 $\hat{y_i} = f(\vec{w} \cdot \vec{x_i} + b)$ ，其中 $f(\cdot)$ 称为激活函数，$ f(\cdot) \in {-1, 1}$ ，损失为 $L_i=\frac{1}{2}(\hat{y_i}-y_i)^2$ 。单层感知机的目的就是习得合适的 $\vec{w}$ 与 $b$ ，使得所有样本的损失之和 $\sum_{x_i \in X} L_i$ 最小。

如果我们令 $z = \vec{w} \cdot \vec{x_i} + b$ 即感知机的输入。那么当 $z < 0$ 时，$f(z) = -1$；当$ z > 0$ 时，$f(z)=1$ 。因为 $z$ 是$x$ 线性组合，所以最终得到的是一个超平面 $\vec{w} \cdot \vec{x}+b=0$ ，超平面将输入样本分为了 $y_i=1$ 和 $y_i=$ -1两类。

当输入 $x=(x_1, x_2)$ 是二维向量时，用红点表示 $+1$ 的数据，黑点表示 $-1$ 的数据，最终习得的是一条直线，将两个数据分离开，如下图所示。

因为单层感知机最终习得是超平面，所以只能用于解决线性可分问题。对于下面这样的数据，单层感知机无能为力。

多层感知机

多层感知机也叫MLP，可以看做是一个有向图。MLP由多层节点组成，每一层全连接到下一层，除输入节点外，每个节点都是一个带有非线性激活函数的神经元（unit）。多层感知机可用于解决线性不可分问题。

因为神经网络的和多层感知器是一个意思，所以下面直接对单层前馈神经网络进行详细说明。

单层前馈神经网络

下图是一个输入层节点数为3，隐藏层节点数为2，输出层节点数为2的前馈神经网络，该网络可用于解决二分类问题。

单层前馈神经网络本质上是一个多层感知机，有以下几个特点：

1. 全连接。每一层的节点都与右边层的所有节点通过权重连接。
2. 隐藏层只有一层。所以称之为单层。
3. 数据单向流动。每一层节点只作用于其之后的层，所以叫作前馈。
4. 本质是数学函数。神经网络可以明确的用数学语言表达。

神经元

我们拿出隐藏层的一个神经元（unit）放大来看：

神经元的任务就是接受输入，产生输出。

z 表示神经元的输入，a 是神经元的输出。

输入怎么得来？就是上一层的神经元输出与权重 的乘积之和再加上偏置。

输出怎么得来？把输入值带入激活函数 得到。

写成数学表达式就是：

$ z^{(2)}1 = w^{(1)}{11}a^{(1)}1+w^{(1)}{21}a^{(1)}2+w^{(1)}{31}a^{(1)}_3+b^{(1)}_1$

$a^{(2)}_1=f(z^{(2)}_1)$

$f(\cdot)$ 是激活函数，常见的有sigmoid、tanh、ReLU。

Sigmoid函数

Sigmoid的表达式为 $S(x)=\frac{1}{1+e^{-x}}$，定义域为 $R$ ，值域为 $(0, 1)$

在 $x=0$ 处，函数值为 $\frac{1}{2}$，其函数图像如下：

sigmoid函数有许多优美的性质，如：

1. 是 $e^x$ 的复合函数，$e$ 又名自然常数

2. 1阶导函数为 $S’(x)=S(x)(1-S(x))$ 。即函数在某一点的导数可由函数在这一点的函数值求得

3. 曲线光滑，定义域内处处可导，且可以无限次求导

4. 可以把任意输入压缩到 $(0, 1)$ 范围内

在反向传播算法（BP算法）中，性质2、3起到了极大的作用，性质4起到了防溢出的作用。

前向传播原理

现考虑一个样本$ (x, y)$ ，其中 $x \in R^3$ 是输入数据，$y \in {[0,1],[1,0]}$是实际值。我们现在来手动计算 $x$ 预测值 $\hat{y}$。预测值 $\hat{y}$ 的计算过程是从输入层开始从左往右计算的，所以这个过程也叫作前向传播。

下图表示，为了得到 $a^{(3)}_1$ ，有哪些神经元被激活了。

为了方便表述，用 $w^{(l)}_{ij}$ 表示第$l$ 层的第 $i$ 个神经元与第 $l+1$ 层的第 $j$ 个神经元相连的权重，用 $b^{(l)}_j$ 表示第$l+1$ 层第 $j$ 个神经元的偏置值。

输入层

注意。输入层没有激活函数，所以：

$[a^{(1)}_1, a^{(1)}_2,a^{(1)}_3]=x$

隐藏层

$ z^{(2)}1 = w^{(1)}{11}a^{(1)}1+w^{(1)}{21}a^{(1)}2+w^{(1)}{31}a^{(1)}_3+b^{(1)}_1$

$ z^{(2)}2 = w^{(1)}{12}a^{(1)}1+w^{(1)}{22}a^{(1)}2+w^{(1)}{32}a^{(1)}_3+b^{(1)}_2$

$a^{(2)}_1=sigmoid(z^{(2)}_1)$

$a^{(2)}_2=sigmoid(z^{(2)}_2)$

输出层

如果我们把 $a^{(3)}_1$ 作为类别为 $0$ 的概率，将 $a^{(3)}_2$ 作为类别为1的概率，则样本 $x_i$ 的预测值可以写成 $\hat{y_i}=\max {a^{(3)}_1, a^{(3)}_2}$ ，所以为了让 $a^{(3)}_1 + a^{(3)}_2 = 1$ ，选用 $softmax$ 作为输出层的激活函数。

$z^{(3)}1=w^{(2)}{11}a^{(2)}1+w^{(2)}{21}a^{(2)}_2+b^{(2)}_1$

$z^{(3)}2=w^{(2)}{12}a^{(2)}1+w^{(2)}{22}a^{(2)}_2+b^{(2)}_2$

令 $g(z^{(k)})=\sum exp({z^{(k)}_i})$，$exp(x)=e^x$

$a^{(3)}_1=softmax(z^{(3)}_1,z^{(3)})=\frac{exp({z^{(3)}_1)}}{g(z^{(3)})}$

$a^{(3)}_2=softmax(z^{(3)}_2,z^{(3)})=\frac{exp({z^{(3)}_2})}{g(z^{(3)})}$

我们令 $\hat{y}_1=a^{(3)}_1$ ，$\hat{y}_2=a^{(3)}_2$，那么 $\hat{y}=[\hat{y}_1, \hat{y}_2]$，同理设 $y=[y_1, y_2]$

神经网络可以明确的用数学语言表达，它的函数表达式，可以明确的写出来

如果真的将这个数学表达式写出来，那么这个数学函数 $network(\cdot)$ 是一个包含 $(3+1) \times 2 + (2+1) \times 2=14$ 个参数的函数，函数输入 $x$ 可得到预测值 $\hat{y}$ ，这个表达式会非常长。

反向传播原理

我们现在来优化网络中这10个权重参数和4个偏置参数。

定义输出层的节点 $i$ 的误差，可用的损失函数有：

1. 均方误差：$E = \sum_{j=1}^2\frac{1}{2} (\hat{y}_j-y_j)^2$
2. 交叉熵损失： $CE=CE(\hat{y},y)=-\sum_{j=1}^{2}y_{j}ln\hat{y}_j$

使用梯度下降算法来优化损失函数，则需要求出损失函数对所有参数的导数，这个过程在计算上是从输出层开始从右往左计算的，因为与计算预测值 $\hat{y_i}$ 的过程恰巧相反，所以也叫作反向传播。

权重的导数

以计算权重 $w^{(2)}_{21}$ 的偏导数为例，根据链式法则不难得到：

$\frac{\partial CE}{\partial w^{(2)}_{21}} = \frac{\partial CE}{\partial \hat{y_1}} \frac{\partial \hat{y}_1}{\partial z^{(3)}_1} \frac{\partial z^{(3)}1}{\partial w^{(2)}{21}}$

∵ $CE=-\sum_{j=1}^{2}y_jln\hat{y}_j=-(y_1ln\hat{y}_1+y_2ln\hat{y}_2)$ ，又 $y_1+y_2=1$，$\hat{y}_1+\hat{y}_2=1$

∴ $CE =-(y_1ln\hat{y}_1+(1-y_1)ln(1-\hat{y}_1))$ （注：这是二分类问题特有的交叉熵表示方式）

∴ $\frac{\partial CE}{\partial \hat{y}_1}=-(\frac{y_1}{\hat{y}_1} - \frac{1-y_1}{1-\hat{y_1}})=\frac{\hat{y}_1-y_1}{\hat{y}_1(1-\hat{y}_1)}$

又 $\frac{\partial \hat{y}_1}{\partial z^{(3)}_1}=\frac{exp(z^{(3)}_1)exp(z^{(3)}_2)}{(exp(z^{(3)}_1)+exp(z^{(3)}_2))^2}=\hat{y}_1\hat{y}_2=\hat{y_1}(1-\hat{y}_1)$

且 $\frac{\partial z^{(3)}1}{\partial w^{(2)}{21}}=a^{(2)}_2$

故原偏导数可写成：

$\frac{\partial CE}{\partial w^{(2)}_{11}}=\frac{\hat{y}_1-y_1}{\hat{y}_1(1-\hat{y}_1)} \cdot \hat{y_1}(1-\hat{y}_1) \cdot a^{(2)}_1=(\hat{y}_1-y_1) \cdot a^{(2)}_2$

更通用化的表达，如何计算 $w^{(2)}_{ij}$ ？依葫芦画瓢得：

$\frac{\partial CE}{\partial w^{(2)}_{ij}} = \frac{\partial CE}{\partial \hat{y_i}} \frac{\partial \hat{y}_i}{\partial z^{(3)}_i} \frac{\partial z^{(3)}i}{\partial w^{(2)}{ij}}=(\hat{y}_j-y_j) \cdot a^{(2)}_i$

令 $\delta^{(3)}_j=\hat{y}_j-y_j$ 表示输出层节点 $j$ 的误差值

则上式可写成：

$\frac{\partial CE}{\partial w^{(2)}_{ij}} =\delta^{(3)}_j \cdot a^{(2)}_i$

如何理解？用 $i$ 表示为隐藏层节点的位置， $j$ 表示为输出层节点的位置，那么权重 $w^{(2)}_{ij}$ 的导数为该权重前一层第i个节点的激活值与后一层第j个节点的误差值的乘积。

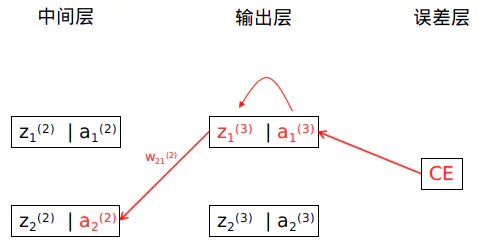
下图是反向传播的示意图，损失函数产生的误差顺着红线一直往左边传，每经过一条红线就求一次导数，直到要求的权重也覆盖在红线为止。下图有三条红线，也就是损失函数 $CE$ 对 $w^{(2)}_{21}$ 的导数需要用三个偏导数乘积形成的链式求导才能得到，且最后一个偏导数值为 $a^{(2)}_i$ 。

如何计算 $w^{(1)}_{ij}​$ 呢？继续使用链式法则 + 依葫芦画瓢可得：

$\frac{\partial CE}{\partial w^{(1)}{ij}} =\sum{k=1}^2((\hat{y}k-y_k)w^{(2)}{jk}) \cdot a^{(2)}_j(1-a^{(2)}_j) \cdot a^{(1)}_i$

令 $\delta^{(2)}j = \sum{k=1}^2(\hat{y}k-y_k)w^{(2)}{jk} \cdot a^{(2)}_j(1-a^{(2)}_j) $ 为 $a^{(2)}_j$ 的误差值 ，那么上式可以写成：

$\frac{\partial CE}{\partial w^{(1)}_{ij}} =\delta^{(2)}_j \cdot a^{(1)}_i$

观察可以发现：

$\delta^{(2)}j=\sum{k=1}^2(\delta^{(3)}jw^{(2)}{jk}) \cdot a^{(2)}_j(1-a^{(2)}_j)$

如何理解？如果用 $i$ 表示输入层节点位置， $j$ 表示隐藏层节点位置，那么权重 $w^{(1)}_{ij}$ 的导数为 该权重前一层第i个节点的激活值与后一层第j个节点的误差值的乘积 。每个节点的误差值 等于 连接权重 与 权重另一端所连节点的误差值 的乘积之和 与 本节点激活值的导数 的乘积。

详细的推导过程读者可以自己琢磨一下，这里有个关键点需要注意：

• 因为 $y_1+y_2=1$，$\hat{y}_1+\hat{y}_2=1$ ，所以 $CE =-(y_2ln\hat{y}_2+(1-y_2)ln(1-\hat{y}_2))$

偏置的导数

如何求 $b^{(2)}_j$ 的导数？根据之前的逻辑推导即可：

$\frac{\partial CE}{\partial b^{(2)}_j} = \frac{\partial CE}{\partial \hat{y_i}} \frac{\partial \hat{y}_i}{\partial z^{(3)}_i} \frac{\partial z^{(3)}_i}{\partial b^{(2)}_j}=(\hat{y}_j-y_j) \cdot 1$

如何求 $b^{(1)}_j$ 的导数？链条太长，这里直接给出答案：

$\frac{\partial CE}{\partial b^{(1)}j}=\sum{k=1}^2((\hat{y}k-y_k)w^{(2)}{jk}) \cdot a^{(2)}_j(1-a^{(2)}_j) \cdot 1$

与权重导数不同的地方就是，在求导过程中的最后一项 $\frac{\partial z^{(l + 1)}_i}{\partial b^{(l)}_j} =1$。

如果加入偏置单元，也可以理解为偏置单元 $a^{(l)}_0$ 的值为1，如下图所示：

正则化项

正则化（regularation）是防止机器学习过拟合的一种手段。一种常见的手段是通过将权重的平方之和加入到损失函数来实现。那么损失函数变为：

$CE=-\sum_{j=1}^{2}y_jln\hat{y}j+\frac{\lambda}{2}\sum_l\sum_i\sum_j(w^{(l)}{ij})^2$

所有权重、偏置之和称为 正则项 ， $\lambda$ 是 正则项系数，也叫 惩罚系数 。

加入正则化项后，$w$ 的导数要多算一个平方项的导数，以 $w^{(2)}_{ij}$ 为例

$grad(w^{(2)}_{ij})=(\hat{y}_j-y_j) \cdot a^{(2)}i+\lambda w^{(2)}{ij}$

向量化

我们假设输入值 $x$ 、 实际值 $y$ 都是列向量。

观察 $ z^{(2)}_1$ 、 $ z^{(2)}_2$ 的表达式，进而发现可以用矩阵形式书写为：

$ \left[\begin{matrix} w^{(1)}{11} & w^{(1)}{12} \ w^{(1)}{21} & w^{(1)}{22} \ w^{(1)}{31} & w^{(1)}{32} \end{matrix} \right]^T \left[ \begin{matrix} a^{(1)}_1 \ a^{(1)}_2 \ a^{(1)}_3 \end{matrix} \right] + \left[\begin{matrix} b^{(1)}_1 \ b^{(1)}_2 \end{matrix} \right]= \left[\begin{matrix} z^{(2)}_1 \ z^{(2)}_2 \end{matrix} \right] $

不失一般性，设第 $l$ 层的前向传播：$z^{(l+1)}=(w^{(l)})^Ta^{(l)}+b^{(l)}$，其中 $a^{(l)}$、$z^{(l+1)}$ 、$b^{(l)}$ 均为列向量， $W^{(l)}$ 为矩阵

激活值 $a^{(l)}=sigmoid(z^{(l)})$，所以激活值也是列向量。

损失函数向量化为：

$CE=-\left[\begin{matrix} y_1 \ y_2 \end{matrix} \right]^T ln\left[\begin{matrix} \hat{y}_1 \ \hat{y}2 \end{matrix} \right] + \lambda(\sum_l\sum_i\sum_jw^{(l)}{ij}+\sum_l\sum_ib^{(l)}_i)$

$=-y^Tln\hat{y}+\frac{\lambda}{2}\sum_{l=1}^2 sum(w^{(l)}*w^{(l)})$

$sum(\cdot)$ 表示把矩阵 $\cdot$ 的所有元素之和

* 表示求哈达马积，即两个矩阵对应位置的元素的乘积所形成的一个新矩阵

输出层误差值向量化：

$ \delta^{(3)}= \left[\begin{matrix} \delta^{(3)}_1 \ \delta^{(3)}_2 \end{matrix} \right]=\left[\begin{matrix} \hat{y}_1-y_1 \ \hat{y}_2-y_2\end{matrix} \right] =\hat{y}-y$

隐藏层误差向量化：

$ \delta^{(2)}= \left[\begin{matrix} (\hat{y}1-y_1)w^{(2)}{11}+ (\hat{y}2-y_2)w^{(2)}{12} \ (\hat{y}1-y_1)w^{(2)}{21}+ (\hat{y}2-y_2)w^{(2)}{22} \end{matrix} \right] * a^{(2)}_j(1-a^{(2)}_j)$

$=\left[\begin{matrix} w^{(2)}{11} & w^{(2)}{12} \ w^{(2)}{21} & w^{(2)}{22} \end{matrix} \right] \left[\begin{matrix} \hat{y}_1-y_1 \ \hat{y}_2-y_2\end{matrix} \right] * a^{(2)}_j(1-a^{(2)}_j) $

$=w^{(2)}(\hat{y}-y) * a^{(2)}_j(1-a^{(2)}_j) $

参数 $w^{(2)}$ 导数向量化：

$ grad(w^{(2)})= grad(\left[\begin{matrix} w^{(2)}{11} & w^{(2)}{12} \ w^{(2)}{21} & w^{(2)}{22} \end{matrix} \right]) = \left[\begin{matrix} \delta^{(3)}_1a^{(2)}_1 & \delta^{(3)}_2a^{(2)}_1 \ \delta^{(3)}_1a^{(2)}_2 & \delta^{(3)}_2a^{(2)}_2 \end{matrix} \right] $

$=\left[\begin{matrix} a^{(2)}_1 \ a^{(2)}_2 \end{matrix} \right] \left[\begin{matrix} \delta^{(3)}_1 \ \delta^{(3)}_2 \end{matrix} \right]^T =a^{(2)}(\delta^{(3)})^T $

不失一般性，有：$grad(w^{(l)})=a^{(l)}(\delta^{(l+1)})^T$

小批量梯度下降

上述所有过程都是假设只有一个样本。

当参与计算的样本数量大于1时：

• 单个损失函数 => 所有样本损失值求平均
• 单个样本的输出层误差 => 所有样本输出层误差求平均

你不用写一个for循环来计算上述值，使用矩阵乘法会更为方便，这里留给读者思考。

实现

github：https://github.com/JerryCheese/machine-learning/tree/master/NN

ann.py 是面向过程版本实现，且隐藏层数只能为1。

NN.py 是面向对象版本实现，支持多层隐藏层。